Wzory na pola figur geometrycznych dla klasy 6 – przewodnik do sprawdzianu

Nauka o polach figur geometrycznych to jeden z kluczowych elementów matematyki w szkole podstawowej. W klasie 6 uczniowie rozszerzają swoją wiedzę na temat różnych figur geometrycznych i uczą się obliczać ich pola. Umiejętność ta jest nie tylko istotna podczas sprawdzianów, ale również niezwykle przydatna w codziennym życiu – od planowania remontu pokoju po projektowanie ogrodu czy wyliczanie kosztów materiałów budowlanych. Poniższy przewodnik pomoże ci usystematyzować wiedzę i skutecznie przygotować się do sprawdzianu z tego ważnego działu matematyki.

Podstawowe pojęcia związane z polami figur

Zanim przejdziemy do konkretnych wzorów, warto przypomnieć sobie, czym właściwie jest pole figury. Pole figury to miara powierzchni, jaką zajmuje dana figura na płaszczyźnie. Wyrażamy je w jednostkach kwadratowych, takich jak cm², m², km² itd.

Przy obliczaniu pól figur korzystamy z różnych elementów, takich jak boki, wysokości, przekątne czy promienie. Kluczowe jest, aby wszystkie wymiary używane w jednym zadaniu były wyrażone w tych samych jednostkach – nie możemy mieszać centymetrów z metrami czy milimetrów z centymetrami. Taki błąd prowadzi do nieprawidłowych wyników, nawet jeśli sam wzór zastosujemy poprawnie.

Ciekawostka: Starożytni Egipcjanie już ponad 4000 lat temu potrafili obliczać pola figur geometrycznych. Było to niezbędne przy odtwarzaniu granic pól uprawnych po corocznych wylewach Nilu, które zacierały oznaczenia granic.

Wzory na pola podstawowych figur płaskich

W klasie 6 uczniowie powinni opanować i umieć zastosować wzory na pola następujących figur:

• Kwadrat – pole obliczamy mnożąc długość boku przez siebie samą: P = a × a = a²
• Prostokąt – pole obliczamy mnożąc długość przez szerokość: P = a × b
• Równoległobok – pole obliczamy mnożąc długość podstawy przez wysokość opuszczoną na tę podstawę: P = a × h
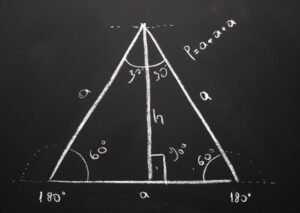
• Trójkąt – pole obliczamy mnożąc długość podstawy przez wysokość opuszczoną na tę podstawę, a następnie dzieląc wynik przez 2: P = (a × h) ÷ 2
• Trapez – pole obliczamy dodając długości podstaw, mnożąc sumę przez wysokość, a następnie dzieląc wynik przez 2: P = [(a + b) × h] ÷ 2
• Romb – pole możemy obliczyć na dwa sposoby: mnożąc długość boku przez wysokość (P = a × h) lub mnożąc długości przekątnych i dzieląc wynik przez 2: P = (d₁ × d₂) ÷ 2

Pole koła i figur związanych z kołem

W klasie 6 uczniowie poznają również wzory na pole koła i figur z nim związanych:

Koło – pole obliczamy mnożąc kwadrat promienia przez liczbę π (pi): P = π × r²

Warto pamiętać, że liczba π jest liczbą niewymierną. W zadaniach szkolnych najczęściej przyjmujemy jej przybliżoną wartość jako 3,14 lub 22/7. Zawsze sprawdź w treści zadania, jaką wartość π należy przyjąć do obliczeń, gdyż może to wpłynąć na końcowy wynik.

Figury związane z kołem

Choć nie zawsze są szczegółowo omawiane w klasie 6, warto znać również:

• Pierścień kołowy – powstaje między dwoma kołami o wspólnym środku. Jego pole obliczamy jako różnicę pól większego i mniejszego koła: P = π × (R² – r²)
• Wycinek koła – to część koła ograniczona dwoma promieniami i łukiem. Jego pole obliczamy jako część pola całego koła: P = (α/360°) × π × r², gdzie α to miara kąta środkowego wyrażona w stopniach.

Praktyczne zastosowanie wzorów – przykłady zadań

Najlepszym sposobem przygotowania się do sprawdzianu jest rozwiązywanie różnorodnych zadań. Poniżej przedstawiam typowe przykłady, które mogą pojawić się na sprawdzianie:

Przykład 1: Oblicz pole prostokąta o długości 8 cm i szerokości 5 cm.
Rozwiązanie: P = a × b = 8 cm × 5 cm = 40 cm²

Przykład 2: Oblicz pole trójkąta o podstawie 12 cm i wysokości 7 cm.
Rozwiązanie: P = (a × h) ÷ 2 = (12 cm × 7 cm) ÷ 2 = 84 cm² ÷ 2 = 42 cm²

Przykład 3: Oblicz pole rombu o przekątnych długości 10 cm i 8 cm.
Rozwiązanie: P = (d₁ × d₂) ÷ 2 = (10 cm × 8 cm) ÷ 2 = 80 cm² ÷ 2 = 40 cm²

Przykład 4: Oblicz pole koła o promieniu 5 cm (przyjmij π = 3,14).
Rozwiązanie: P = π × r² = 3,14 × 5² = 3,14 × 25 = 78,5 cm²

Zadania złożone i nietypowe

Na sprawdzianach z pól figur w klasie 6 często pojawiają się zadania, w których trzeba wykazać się nie tylko znajomością wzorów, ale również umiejętnością łączenia wiedzy z różnych działów matematyki:

• Figury złożone – czasem trzeba obliczyć pole figury, która składa się z kilku prostszych figur. Wtedy najczęściej obliczamy pola poszczególnych części i je sumujemy lub odejmujemy. Na przykład, pole figury w kształcie litery L można obliczyć jako sumę pól dwóch prostokątów lub jako pole dużego prostokąta minus pole brakującego prostokąta.
• Zadania z niewiadomymi – mogą pojawić się zadania, w których znamy pole figury i jeden z wymiarów, a musimy obliczyć drugi wymiar. Wymagają one przekształcenia wzoru na pole danej figury.
• Zadania tekstowe – często sprawdzają umiejętność zastosowania wiedzy o polach figur w praktycznych sytuacjach, np. obliczanie kosztu malowania ściany, układania płytek czy wykładziny, wyliczanie ilości potrzebnej tapety czy farby.

Strategie rozwiązywania zadań na sprawdzianie

Podczas przygotowań do sprawdzianu z pól figur warto stosować następujące strategie:

• Zapamiętaj kluczowe wzory – upewnij się, że znasz wszystkie wzory na pamięć i rozumiesz, co oznaczają poszczególne symbole. Pomoże ci to szybciej rozwiązywać zadania podczas sprawdzianu.
• Rysuj pomocnicze szkice – przy rozwiązywaniu zadań często pomocne jest narysowanie figury i zaznaczenie na niej wszystkich znanych wymiarów. Nawet prosty szkic może znacznie ułatwić zrozumienie problemu.
• Zwracaj uwagę na jednostki – pamiętaj, by wszystkie wymiary były wyrażone w tych samych jednostkach, a wynik podawaj w jednostkach kwadratowych. Jeśli w zadaniu podano wymiary w różnych jednostkach, najpierw zamień je na jedną wspólną jednostkę.
• Sprawdzaj wyniki – po obliczeniu pola zastanów się, czy wynik jest sensowny. Na przykład, jeśli obliczone pole pokoju wyszło 2 cm², to z pewnością popełniłeś błąd, gdyż jest to wartość zdecydowanie za mała dla pomieszczenia.

Przygotowanie do sprawdzianu z pól figur geometrycznych wymaga systematycznej pracy i rozwiązywania różnorodnych zadań. Warto poświęcić czas na zrozumienie wzorów i ich zastosowań, ponieważ ta wiedza będzie wykorzystywana również w kolejnych latach nauki matematyki. Pamiętaj, że najważniejsze jest nie tylko zapamiętanie wzorów, ale przede wszystkim zrozumienie, skąd się one biorą i kiedy należy je stosować. Dzięki temu będziesz w stanie rozwiązać nawet nietypowe zadania, które mogą pojawić się na sprawdzianie.